ㅁ Logistic Regression
o Supervised Learning으로 Classification 문제를 해결하며 2범주 문제를 다룬다.
- 회귀분석으로 분류문제를 해결한다.
- 로지스틱 회귀분석이 끝나면 결과물이 확률로 나와야 한다.
o A와 B, 두 카테고리 중 하나로 분류한다.
- 선형 회귀분석 식에서
- 우리가 예측하려는 Y값을 A일 확률로 가정하고,
- Y값(A일 확률)이 0.5보다 크면 A로 분류하고, 0.5보다 작으면 B라고 분류하면 되지 않나!
ㅁ 수식 전개
선형회귀식 $$ y = ax + b $$
y를 확률로 변환 $$ P = ax = b $$
이때 양변이 갖는 값의 범위가 일치하지 않는다.
선형 회귀식은 0 ~ 1 범위이지만 확률은 무한대의 범위를 가지기 때문
그리고 범위를 맞추기 위해 다음와 같이처리한다.
P 자리에 Odds를 대입 $$ Odds = P/(1-P) = ax + b $$
여전히 양변의 값의 범위가 일치하지 않는다.
여기서 Odds에 Log를 씌운다.$$ log_e{Odds} = log_e{P/(1-P)} = ax + b $$
양변의 값의 범위가 일치하게 된다.
위에서 도출한 식에서 확률 P를 구해야 하니까 Odds로 표현된 식에서 P로 정리한다.
$$ log_e{P/(1-P)} = ax + b $$
양변에 e를 씌움 $$ e^{log_e{P/(1-P)}} = e^{ax + b} $$
그리고 한번 더 정리하면 $$ P/(1-P) = e^{ax+b} $$ 가 된다.
역수를 취함
$$ (1-P)/P = 1/e^{ax+b} $$
$$ 1/P - 1 = 1/e^{ax+b} $$
1을 더함
$$ 1/P = 1/e^{ax+b} + 1 $$
$$ 1/P = (1+ e^{ax+b}) / e^{ax+b} $$
역수를 취하면 다음과 같이 P로 정리가 된다.
$$ P = e^{ax+b} / (1+e^{ax+b}) $$
위의 식에서 a,b,x,e 4개를 알면 P를 구할 수 있다.
선형회귀 분석식에서 기울기랑 절편 구하는 공식을 적용하면 되고,
a랑 b는 데이터가 있으면 구할 수 있다.
x는 입력값이니까 입력하면 되고, e를 2.718로 계산한다.
그럼 이제 식을 도출할 수 있다. 계산을 하면 다음과 같은 그림이 그려진다.
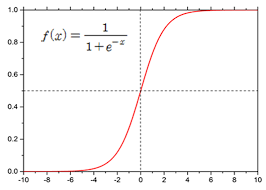
Logistic Curve가 나온다.
여기서 P는 0.5를 기준으로 0.5보다 크면 A로 분류하고, 작으면 B로 분류한다.
무조건 0과 1 사이의 값이 나오지만 0과 1은 절대로 나오지 않는다.
'Develop > AI' 카테고리의 다른 글
| 인공지능(신경망, 딥러닝) 교육 정리(Differential, 미분) (0) | 2023.01.01 |
|---|---|
| 인공지능(신경망, 딥러닝) 교육 정리(Python, 객체지향(with.Java)) (0) | 2023.01.01 |
| 인공지능(신경망, 딥러닝) 교육 정리 (Linear Regression) (0) | 2022.12.28 |
| 인공지능(신경망, 딥러닝) 교육 정리 [Linear Classifier] (0) | 2022.12.28 |
| 인공지능(신경망, 딥러닝) 교육 정리 [Decision Tree] (0) | 2022.12.28 |







최근댓글