인공지능(신경망, 딥러닝) 교육 정리(Differential, 미분)

ㅁ Differential, 미분, 변화

 o 미분은 순간 기울기를 구하기 위함이다. 내가 이만큼 변하면 쟤는 얼만큼 변하는지 알 기 위해
  - 하나의 변화가 다른 하나에 어떤 영향을 끼치는가?
  - 시간에 변화에 따른 자동차 속도의 변화, 일조량에 따른 수확량의 변화. 
  - 상수는 변하지 않는 값이기 때문에 바뀌는 값을 찾는 미분에서는 안써먹히니 버리는 것이다.

 

ㅁ 자동차 예제

 o 시간에 따라 속도의 변화가 없는 경우
  - s = 40 
  - 시간의 변화에 따라 속도는 어떻게 변하는가? 0이다. 

 

 o 일정한 비율로 증가 
  - 속도가 일정한 비율로 증가
  - s = 40 + t 

 

 o 정지상태에서 차량 출발
  - 어떤 순간에 속도의 변화율은 얼마인가?
  - 국선에서는 어떻게 적용 되는 것인가?
  - s = t^2

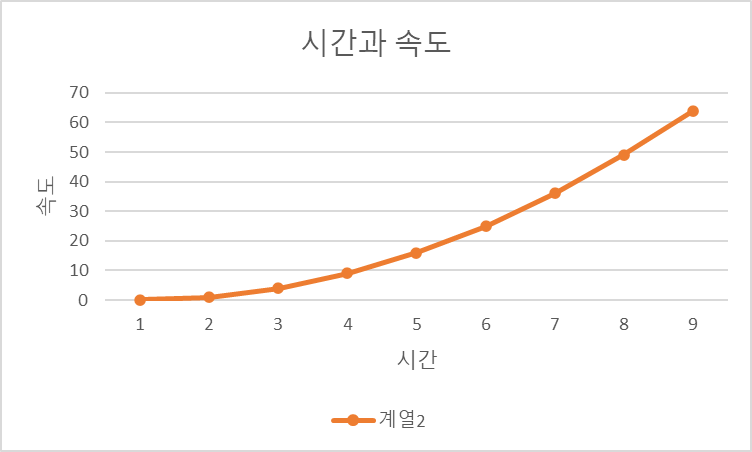
 - 위의 표에서 3분의 기울기 < 6분의 기울기다.
 - 어떤 순간의 변화율 = 그 순간에서의 곡선의 기울기
 - 그리고 이것은 탄센트를 많이 구한다. 

 o 디테일한 미분 검증은 수학시간에... 다시 한번 생각해보는 것으로 하고... 미분공식은 다음과 같다.

미분 공식

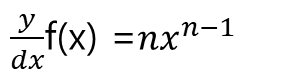
 - 여러 미분 공식이 쓰이니까 미분 공식은 알아두어야 할 것 같다. 

f(x) + g(x)

지수의 밑수 a가 임의의 실수인 지수함수

자연로그 함수의 도함수

지수의 밑수 a가 자연상수 e인 지수함수

 

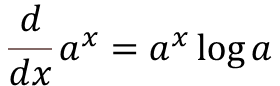
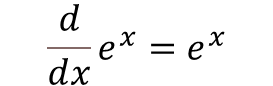
 o 합성함수(중첩된 함수)

y의 변화에 따라 f는 어떻게 변화 하는 것인가? 아래와 같이 표현 가능하다.

x의 변화에 따라 f는 어떻게 변화하는가? 아래와 같이 표현가능하다. 

처음단계에서 마지막으로 한번에 미분하면 안되고 한차례 건너서 미분해야한다. 
f를 y로 미분하고, y를 x로 미분해야한다.

오차가 변하면 가중치도 변하지 않냐?
미분이 왜 필요하겠니? 변화량을 알아야하기 때문이고, 그 변화량이 여러개가 나온다. 
ex out의 W의 가중치를 변경했더니 hidden의 W 가중치도 변한다.
내가변했을때 너는 얼마나 변하는가? 를 미분에서 도출할 수 있으니까 필요하다.

중첩된 함수 계산하는방법

 

위의 계시로 계산한 내용이다. 잘 고민해보시게ㅎㅎ

 

ㅁ 편미분

 o 독립적인 변수(x,y,z는 서로 독립)