인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 1)

ㅁ Artificial Neural network Neuron 작동원리

 o 뉴런세포에 착안하여 만든 알고리즘으로 어떤 데이터를 취합하고 그 값을 활성함수에 넣어서 0과 1의 활성함수로 도출한다. 
 o 퍼셉트론에서는 step함수를 활성함수를 사용했다. 하지만 step 함수는 인공신경망에서 사용할수가 없다.

.

 o 퍼셉트론에서는 step함수를 활성함수를 사용했다. 하지만 step 함수는 인공신경망에서 사용할수가 없다.
  - 0과 1 밖에 안나오기 떄문에
 o 흔히들 가장 기본적으로 쓰는 함수는 sigmoid 함수이다. 아웃풋이 무한대에서 가능하기 떄문이다. 

sigmoid function

---

ㅁ Artificial Modeling

 o 구조 : 각 뉴런을 상호연결 

그리기 너무 귀찮은 그림

 o 신경망 구조에서 어떤 부분이 학습이 되는 것일까?
 o 학습은 어떻게 일어나는 것일까?
 o 선형 모델의 기울기 같은 업데이트 되는 값이 있는가??
  => 노드 간의 연결 강도 조정 필요 = 연결 강도 조정이 가중치를 업데이트 하는 것이다.

 o 가중치의 표현은 다음 그림과 같이 할 수 있다.

가중치의 표현

---

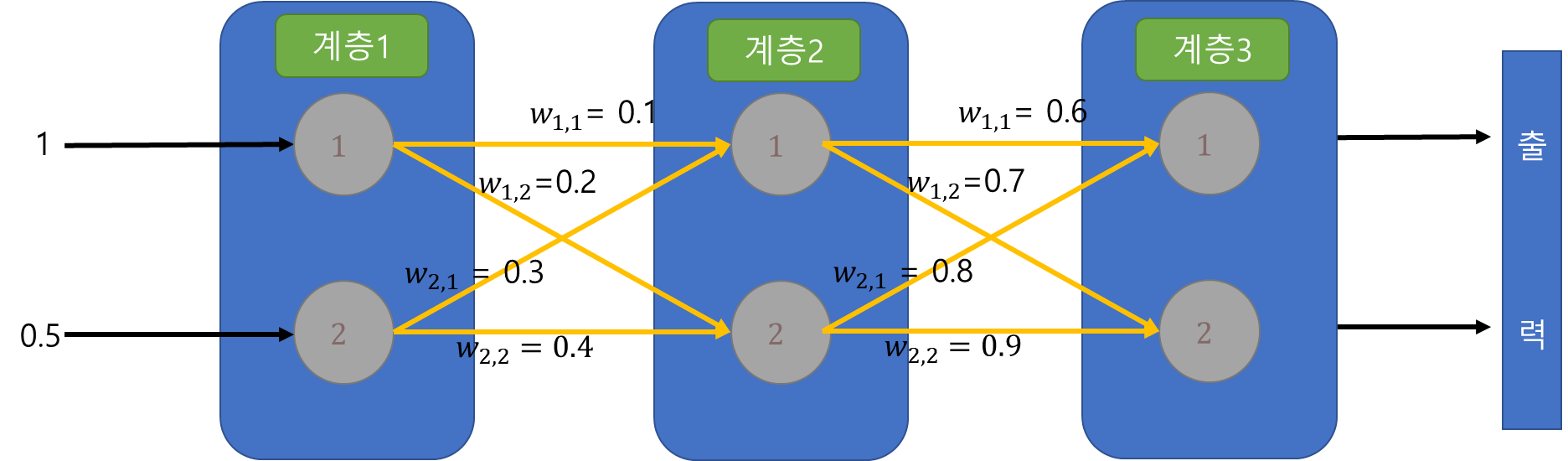
ㅁ 2계층 네트워크를 통해서 가중치 계산을 진행해보자 

 o 2계층 네트워크 표현 그림

Random Weight
w1.1 = 0.9	w1.2 = 0.2
w2,1 = 0.3	w2,2 = 0.8

 o 위의 내용을 기반으로 계산식을 전개해볼 수 있다. 계산은 맨 위의 그림을 통해 도출 할 수 있다.
  -  입력값은 우리가 임의로 줄 수 있기 때문 입력 값은 1.0과 0.5로 설정한다.

입력값으로 1과 0.5를 준다 그럼 계층1의 input은 정해지고 이제 계층2를 구해야한다.
wi와 xi를 구해야하니까 계층2의 값은 계층1에서 1과 2에서 오는 값을 더해야한다. 그래야 계층2의 입력값이 나온다.
위의 그림에 따르면 그 결과가 그대로 출력으로 나오게 된다.
수식을 전개하면 다음과 같은 식이 나온다.
$$ OUTPUT1 => intput1 * W_{1,1} + input2 * W_{2,1} => (1.0 * 0.9 ) + (0.5 * 0.3) => 1.05 $$
$$ OUTPUT2 => input1 * W_{1,2} + input2 * W_{2_2} => (1.0 * 0.2) + (0.5 * 0.8) => 0.6 $$

시그마Wi,Xi를 구했으니까 여기서 활성함수인 시그모이드 함수를 적용하면 다음과 같은 값이 나온다.
O1 = 0.7408, O2 = 0.6457

---

위의 식을 보니까 (곱셈하고 더하고)를 반복한다. 그러면 이것을 행렬로 바꿀 수 있지 않을까?

 

바로 위에 있는 표를 가지고 행렬로 만들어보자. 그럼 아래와 같이 표현이 가능할 것이다. 

학생때 배운 행렬이 또 이렇게 쓰일줄은 상상도 못했다.

먼저 계층1의 계산부터 해준다 입력값이 1.0 과 0.5가
들어왔으니까 이것을 그대로 표현하면 다음과 같다. 

가중치 * 입력값 = 출력값 => 출력값 * Sigmoid => 최종 출력값

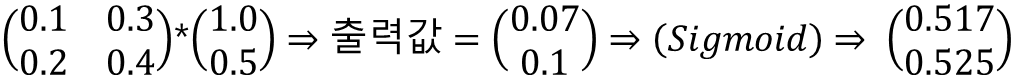
계층1의 출력값(O)를 구했다. 위의 그림을 보면 그 출력값이 다시 계층2의 입력값으로 들어간다.
그럼 계층2 기준으로 입력값을 바꾸어서 위의 계산을 다시 수행하면 최종 출력값이 나오게 될 것이다.

---

이렇게 행렬 곱을 사용하면 크기에 상관없이 신경망을 간단하게 표현할 수가 있다.
행렬로 표현할땐 입력계층을 세로로 입력하고 가중치 행렬을 적을떄도 헷갈리지 않고 잘 적어야한다.

간단하게 2계층수준으로만 했지만 노드도 3개로 하고 3계층으로해도 충분이 계산이 다된다. 

모 대충 이렇게 표현이 가능할 것이다.