ㅁ Weight update
o 인공신경망에서 가중치업데이트는 어떻게 하고 있지?
o 현재 역전파되는 오차까지 계산이 된다.
o 오차는 가중치를 조절해 가는데 아주 중요한 지표이다.
o 신경망의 오차
- 단순한 선형 분류자가 아니다.
- 각 노드에 입력과 갖우치를 곱하고 합한 후 활성함수를 통과
- 각각의 노드를 연결하는 가중치의 업데이트는 정교한 계산이 필요하다.
o 그렇다면 가중치는 계산이 가능한가?
- 각각의 노드를 연결하는 가중치는 서로 연결이 되어 잇다.
- 하나를 수정하면 나머지 노드의 가중치가 모두 영향을 받는다.
- 대수학적인 접근이 어렵다.
- 그래서 완전탐색(블루트포스)으로 해보면 500개의 노드를 가지는 3계층 신경망으로 예시로할때 총 5억 가지에 대해 테스트하는데, 하나의 조합 연산시간을 1초로 해도 하나의 가중치를 업데이트하는데 16년이나 필요하다
o 수학적인 접근이 어려울 때 가중치는 어떻게 구하지?.
- 수식 자체가 어렵고 가중치의 조합이 너무 많아 최적의 조합 테스트가 어렵다.
- 학습 데이터가 충분하지 않고 데이터 자체의 오류도 포함 되어있어 수학적 접근을 더 어렵게 한다.
o 위의 한계점때문에 경사 하강법을 사용한다.
- 어두운 산에서 렌턴하나 있을때 어떻게 산을 내려 올것인가? 앞에 보이는 만큼에서 가장 안전해보이는 길로 내려온다.
- 경사는 지형의 기울기를 의미하고 복잡한 산의 지형을 수학의 함수라고 생각한다.
* 함수가 너무 복잡해 대수학으로 함수의 개요를 파악하지 못할떄
* 경사 하강법을 이용해 단계적인 접근 가능
* 정확한 답은 못찾아도 현재보다는 조금씩 더 좋은 답을 찾아갈 수 있음
o 그렇다면 경사하강법과 신경망은 무슨 연관성이 있나?
- 복잡한 함수를 신경망의 오차로 생각한다.
- 함수의 최저점을 찾는 과정을 오차를 최소화 하는 과정으로 치환
- 이를 통해 신경망의 성능을 개선해본다.
$$ y = (x-2)^2 + 1 $$
음의 기울기일때 x축의 오른쪽 방향으로 이동 => x값이 증가
양의 기울기일때 x축의 왼쪽 방향으로 이동 => x값 감소
미분해서 기울기가 음수면 x를 오른쪽으로 움직이고, 양수면 x를 왼쪽으로 땡기면 가장 최저점을 찾을 수 있다.
=> 그렇다면 기울기의 보폭은 어떻게 설정하지?
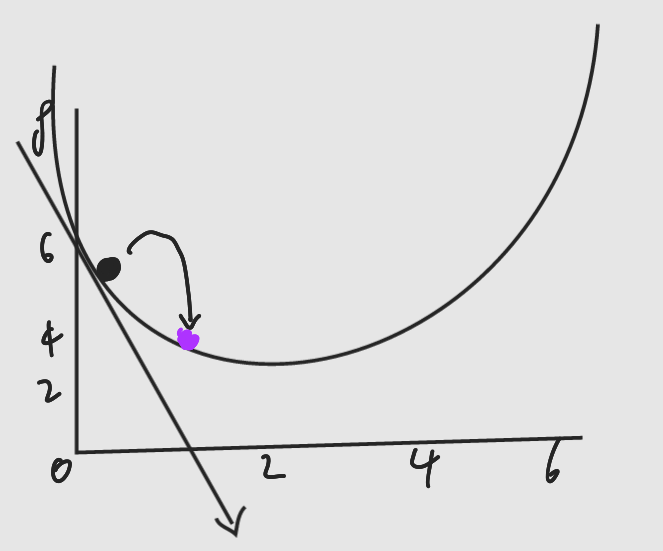

내려올때 보폭을 잘 조절해야한다.
항상보폭이 일정하면 최저점 근처에서 최저점을 지나가는 현상이 발생한다.
최저점에 가까울 수록 기울기가 완만해짐 -> 기울기가 완만해질수록 보폭을 줄이면 되지 않나!?

많은 파라미터를 가지고 있는 함수인 경우 문제가 발생할 수 있다.
여러 곳의 계곡이 있으면 가장 깊은 계곡보다 다른 곳으로 갈 수도 있다.
이것을 해결하기 위해
각각 다른 출발 위치에서 시작해 실험을 여러 번 하는 것으로 해결한다,
가중치의 초기 값을 하나로 하지 않고 다르게 주면 된다.
(이를 위해 입력값은 랜덤으로 중복없이 돌린다)
하지만 이것도 운이 나쁘면 찾을수가 없다.
ㅁ Error Function
o 신경망의 결과함수 자체는 오차함수가 아니다.
o 오차는 목표 값(Target Value)와 모델 결과값(network Output)과의 차이이다.
o 그러면 결과값을 기반으로 오차함수를 구할 수 있다.
o 사용 가능한 오차함수(Error Function)
| 모델결과값 | 목표 값 | 오차1 (목표 값 - 모델 결과값) |
오차2 | 목표 값 - 모델결과값 | |
오차3 (목표값 - 모델결과값)^2 |
| 0.3 | 0.5 | 0.2 | 0.2 | 0.04 |
| 0.9 | 0.9 | 0 | 0 | 0 |
| 0.6 | 0.4 | -0.2 | 0.2 | 0.04 |
| 총합 | 0 | 0.4 | 0.08 | |
오차1의 경우 상쇄가 되서 쓸수가 없다.
실제로 머신러닝을 돌릴때 1이 나오는 경우는 거의 없다. 그래도 잘 쓰지 않는다.
오차가 상쇄됨으로써 좋은 방법은 아니다.
오차2의 경우 오차가 상쇄되는 문제는 해결할 수 있다.
근데 최저점 근처에서 연속적이지 않고 미분할 수가 없다(그래프 모양이 V자 모양이 나오면 미분할 수 없음)
최저점 근처에서 기울기가 작아지지않기때문에 오버슈팅이 일어날 가능성이 매우 높음
오차3의 경우 제곱오차방법이다.
경사 하강법으로 기울기를 구할때 수식이 간단해 지고, 오차함수가 연속되어 잘 작동한다.
최저점 근처에서는 경사가 작아지므로 오버슈팅의 가능성이 작아진다.
위의 오차를 구하는 방식으로 사용할 수 있는 것은 합했을때 0이 안나오고 미분이 가능하면 위의 방법이외에도 다양하게 적용할 수 있다.
ㅁ 경사하강법 사용
o 가중치에 대한 오차함수의 기울기를 구해야함.
o 기울기는 미분으로 구함
- 하나가 변할때 다른 것의 변화에 얼마나 영향을 끼치는가?
- 신경망에서 오차함수는 가중치의 변화에 얼마나 영향을 받는가?
* 가중치의 변화에 따라 오차는 얼마나 변하는가?

가중치 Wij의 값의 변화에 따라 오차 E값이 얼마나 변하는가?
최저점 방향으로 이동하며 감소하는 것을 기대하는 오차함수의 기울기
3차원 이상의 상황에서는 2개 이상의 가중치가 존재한다.
경사하강법으로 최저점을 찾아가는 방법은 동일하다.

노드 오차 = 목표 값 - 실제 값 $$ e_k = t_k - o_k $$
노드오차 = 에러 - 아웃풋
가중치 업데이트를 하는 최종 수식이다.

위의 수식이 나오는 이유를 하나하나 설명하고 싶은데, 설명하기가 너무 귀찮...다...
(무엇보다 깔끔하게 표현하기위해 작성하는 것이 너무너무 귀찮...다..

오직 연결된 가중치의 영향만을 받음
따라서 연관이 없는 노드의 연결은 표현하지 않아도 되므로 시그마 기호는 삭제한다.

연세법칙을 이용해서 미분을 적용한다.
이전식에서 tk(목표값)은 상수이며, wjk값이 변하더라도 불변이다.
tk는 wjk의 함수가 아니며, 오직 wjk에 영향을 받는 ok처리가 필요하다.
오른쪽 사각형은 미분하는 순서이다.

Oj는 최종 출력 계층의 출력값이 아닌 직전 은닉 계층 노드로부터의 출력값이다.
입력 신호의 가중치 합에 sigmoid 함수 적용 한 것이다.
이후 추가 전재가 있긴하지만.. 못쓰겠다 스킵.
가중치 업데이트를 하는 최종 수식해서 입력계층과 은닉계층 사이에 있는 가중치는
기존 결과식에서 첨자만 변경하면 된다. (하나씩 땡기면 되는거잖아)

ㅁ Leraning Rate
o 최저점 근처에서 오버슈팅을 피하기 위해 사용한다.
o 데이터의 오차를 줄일 수 있다.
o 가중치업데이트 수식

새로운 가중치는 계산으로 구한 오차 기울기에 상수(a)를 곱하고 이를 이전 가중치에서 빼줌
빼는 이유는 양의 기울기일때는 가중치를 줄이고, 음의 기울기 일때는 가중치를 늘리기 위해서
= > 가중치는 기울기와 반대로 움직임
곱해주는 상수 값 a 가 학습률이다.
신경망에서는 빼기로 해야한다
(기존에는 더했지만 w가 양수면 x가 음의방향이고 w가 음수면 x가 양의 방향이기때문에)

생각해두어야 할 점
신경망의 오차는 가중치의 함수로 표현 가능하다.
신경망을 업데이트 한다는 것은 가중치를 변화시켜 오차를 줄여 나가는 것을 의미
경사하강법을 이용해 점진적으로 오차를 줄여 최적의 결과를 도출
미분을 사용하여 오차의 기울기를 계산할 수 있음
복잡해 보이나 개념을 따라가면 충분히 이해 가능하다.
은닉계층과 출력계층 사이의 w11 업데이트
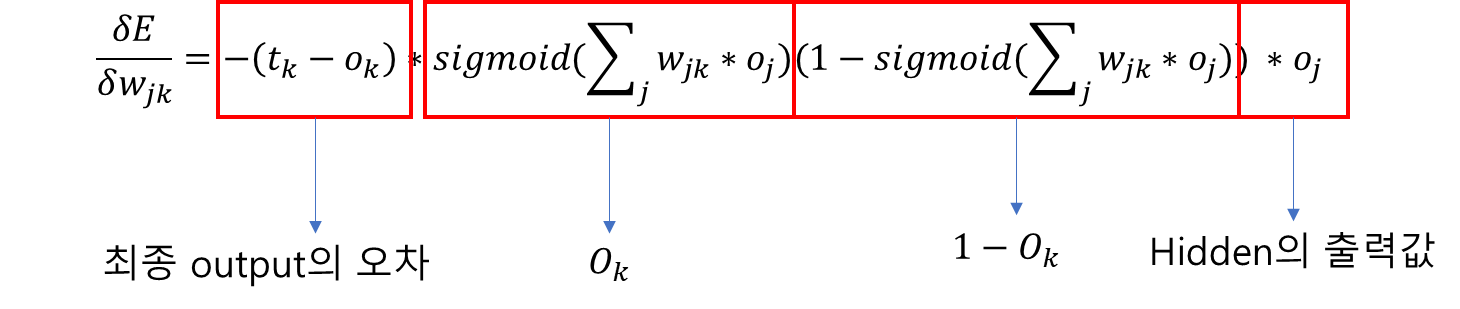

(tk - Ok) 는 오차 e1이다. e1는 0.7
시그마Wjk * Oj = (1.0 * 0.4) + (3.0 * 0.6 ) = 2.2
Sigmoid 값 = 0.9002
0.9002 * (1 - 0.9002) = 0.089
Oj 값은 j가 1일때 가중치 w11에 관심
Oj=1 =0.4
정리하면 다음과 같이 할 수 있다.
-(0.7 * 0.089 * 0.4) = -0.02492
학습률이 0.05라고 하면 (0.05 * -0.02492)
새로운 w11는 (1.0 - (-0.001246)) = 1.001246
위 예제의 결과를 보면 가중치가 1.0에서 1.001246으로 아주 작은 값으로만 변한다.
작은 변화이지만 이를 굉장히 많이 반복하게되면 점점 최적 값으로 수렴한다.
이렇게 신경망이 학습을 진행하여 좋은 결과 값을 유도하게한다.
현재 많은 tools와 프로그램 언어를 통해 간단히 모델을 만들어 실험할 수 있다.
신경망이 항상 잘 작동하는 것은 아님
학습이 잘되도록 여러 값의 디자인이 필요하다.
신경망이 잘 동작하지 않을때의 대표적인 이유는
학습 데이터, 가중치의 초기값, 결과값의 범위 등을 잘못 잡았을 경우가 많다.
위를 잘 정리하면 성능이 좋아 질 수 있다.
'Develop > AI' 카테고리의 다른 글
| 인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 3) (0) | 2023.01.15 |
|---|---|
| 인공지능(신경망, 딥러닝) 교육 정리 (Preparing Data) (0) | 2023.01.08 |
| 인공지능(신경망, 딥러닝) 교육 정리 (Backpropagation) (0) | 2023.01.08 |
| 인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 1) (0) | 2023.01.08 |
| 인공지능(신경망, 딥러닝) 교육 정리(single Layer Perceptron) (0) | 2023.01.02 |







최근댓글