Preparing data
ㅁ 포화(Saturaion)
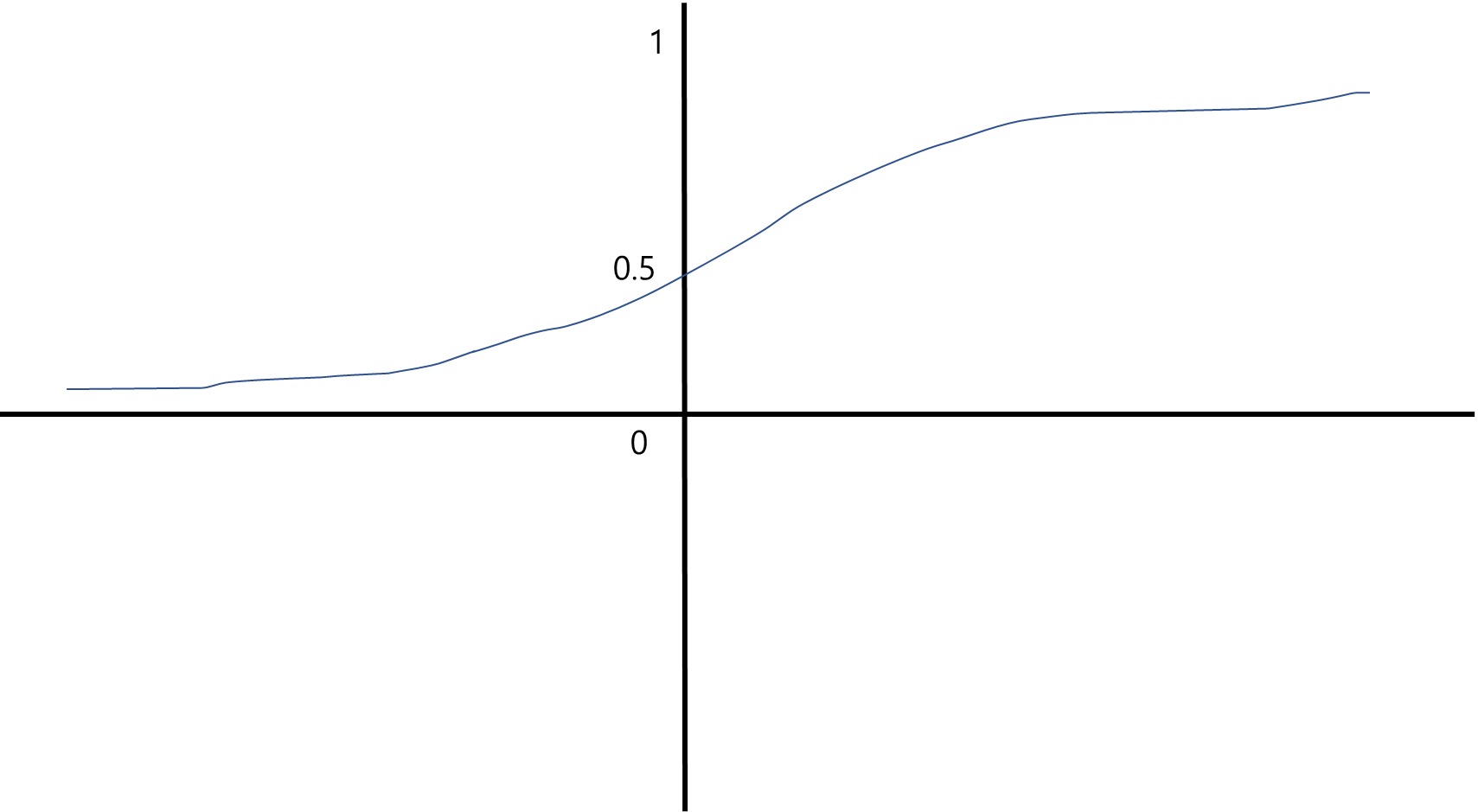
ㅁ Input Data
o 입력값(x)이 클 경우 그래프 양 끝단의 기울기가 평평한 형태가 된다
o 가중치의 변화는 활성함수의 기울기에 영향을 받는다.
o 신경망의 한계로 변화값이 너무 작아져서 변화가 나오지 않는다.
- 양 끝단에 들어가면 업데이트가 안되는 것을 포화라고 한다.
o 기울기가 작아져 학습이 제한되는 것.
o 입력 시 입력 값(x값)을 작게 유지 해야함
o 가중치를 너무 작게 만들어도 정확도를 잃어버림
o 입력 값을 0.0 ~ 1.0 사이의 값이 오도록 조정
o 0.01같은 작은 값을 더해 입력이 0이 들어오는 것을 막기도함
o 이 문제는 학습중에 언제 저기로 빠지는지 알수가 없다.
o 포화상태를 20년간 해소를 못했고, 포화상태를 막거나 탈출할 수 있는 방법을 못찾았다.
o 그렇다고 성능이 안좋은게 아니라 개선할 부분이 많은 것이다.
o 무한한 값을 유한한 값으로 한정지었기 때문에 오차가 발생할 수 있다.
o 너무너무 작은 값이 들어오면 컴퓨터의 한계상 일부 바뀔 수도 있다.
o 입력 데이터를 만들때 아주 작은 수를 추가로 더해준다. 0이 안나오게 하려고,
o 입력 데이터는 너무 큰 수도 안되고 너무 작은 수도 안되고 0도 안된다.
o 시그모이드 함수를 쓴다면 0 ~ 1 사이에서만 결과가 나온다.
ㅁ Output Data
o 신경망의 결과 값은 마지막 계층에서 나오는 출력 신호
o 로지스틱 함수는 결과가 1.0을 넘지 못함
o 점근적으로 1.0에 접근함 따라서 출력값이 1.0이나 0.0보다 작은 값은 사용할 수 없음
o 만약 도달 불가능한 영역의 값을 목표 값으로 선정한다면 가중치가 점점 커져서 결국 신경망이 포화에 걸림
-> 목표값을 도달 불가능한 값으로 선정할 수 없음
o 0.01 ~ 0.99 사이의 값으로 사용
ㅁ Random Initial Weights

o 가중치도 초기화 시 큰 값의 입력을 피해야 함
o 가중치의 초기화는 -1.0 ~ 1.0 사이의 임의의 값
o 입력 데이터는 우리가 전처리 등을 해서 건드릴 수 있다. 근데 가중치는 노드의 개수가 많아지면 가중치 값을 작게 주더라도 곱의 합도 많아져서 값이 커질 수 밖에 없다.
o 그래서 가중치가 많아지면 폭을 줄이고, 가중치의 개수가 적으면 폭을 넓히는 방법이 없을까?
o 그래서 수학에 있는 정규 분포를 가지고 와서 활용한다.
o 수학적으로 찾아낸 가중치의 값이 있다.

o 노드가 많아지면 많아질수록 폭은 좁아진다.
o 가중치의 초기 값은 같은 상수로 초기화하면 안된다.
o 미분이 가지는 약점을 그대로 가지고 있기 때문이다. 웅덩이가 여러개 있는데, 작은 웅덩이에 들어가도 멈춘다
o 제일 오차가 작은 점을 찾아야하는데, 작은 웅덩이 들어가면 멈추니까 가중치 값은 계속 바꿔줘야 한다.
o 0으로 입력하는 것도 절대 불가!
'Develop > AI' 카테고리의 다른 글
| 인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 4) (0) | 2023.01.15 |
|---|---|
| 인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 3) (0) | 2023.01.15 |
| 인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 2) (0) | 2023.01.08 |
| 인공지능(신경망, 딥러닝) 교육 정리 (Backpropagation) (0) | 2023.01.08 |
| 인공지능(신경망, 딥러닝) 교육 정리(Artificial Neural Network 1) (0) | 2023.01.08 |







최근댓글