ㅁ 개요
o 예측과 분류는 기업들이 가장 알고 싶어하는 주제이다
o 예측모델은 구체적으로 어떻게 만들어 지는가?
- 과거 데이터를 기반으로 미래 예측
- 객관성 담보 -> 수학으로
- 구체적인 접근방법을 고민 -> 수치형 데이터로 변환 가능한가?
o 예측과 분류 모델은 바로 현업에 적용이 가능한 것인가?
o Entropy가 무엇인가?
o Decision Tree가 무엇인가?
ㅁ 접근방법
o Supervised Segmentation
o Target Value 에 가장 강한 영향력을 끼치는 Attritube는?
o 영향력을 수치형 데이터로 바꿀 수 있을까?
- 이때 사용 가능한 수학개념은?
- 영향력을 수치형 데이터로 바꿀 수 있따면 가능한 작업은 무엇이 있을까?
o 각 속성이 Target Value에 끼치는 영향력은?
- 영향력을 수치형 데이터로 구할 수 있는가? -> 그럼 정렬이 가능한가? -> 그럼 가능한 작업은 무엇이 있나?
- 수학 사용 근거의 개념 연결 고리가 필요하다.
| Attribute | Target Value | ||||||
| 나이 | 직장 | 잔고 | 거주형태 | .... | 상환여부 | ||
| Instance | 김씨 | 25 | 대기업 | 500만원 | 월세 | O | |
| Instance | 이씨 | 28 | 중견 | 1억 | 전세 | X | |
| Instance | 최씨 | 44 | 개인 | 20억 | 자가 | O | |
* Feature Selection : 논문이 엄청 많이 나오고, 모든 알고리즘에서 사전 전처리가 다 들어간다. 몸 값을 높이기 위해 피쳐셀렉션도 잘하면 좋은데, 수학적 역량이 필요하다.
ㅁ Entropy과 Information Gain 계산
o 어떤 집합에 대한 무질서한 정도를 측정
o 엔트로피는 물리학에서 사용하는 개념이고 1에 가까울수록 안정적인 상태이다.
o 왜 데이터 분석에 엔트로피가 접목이된 이유는 무엇인가?
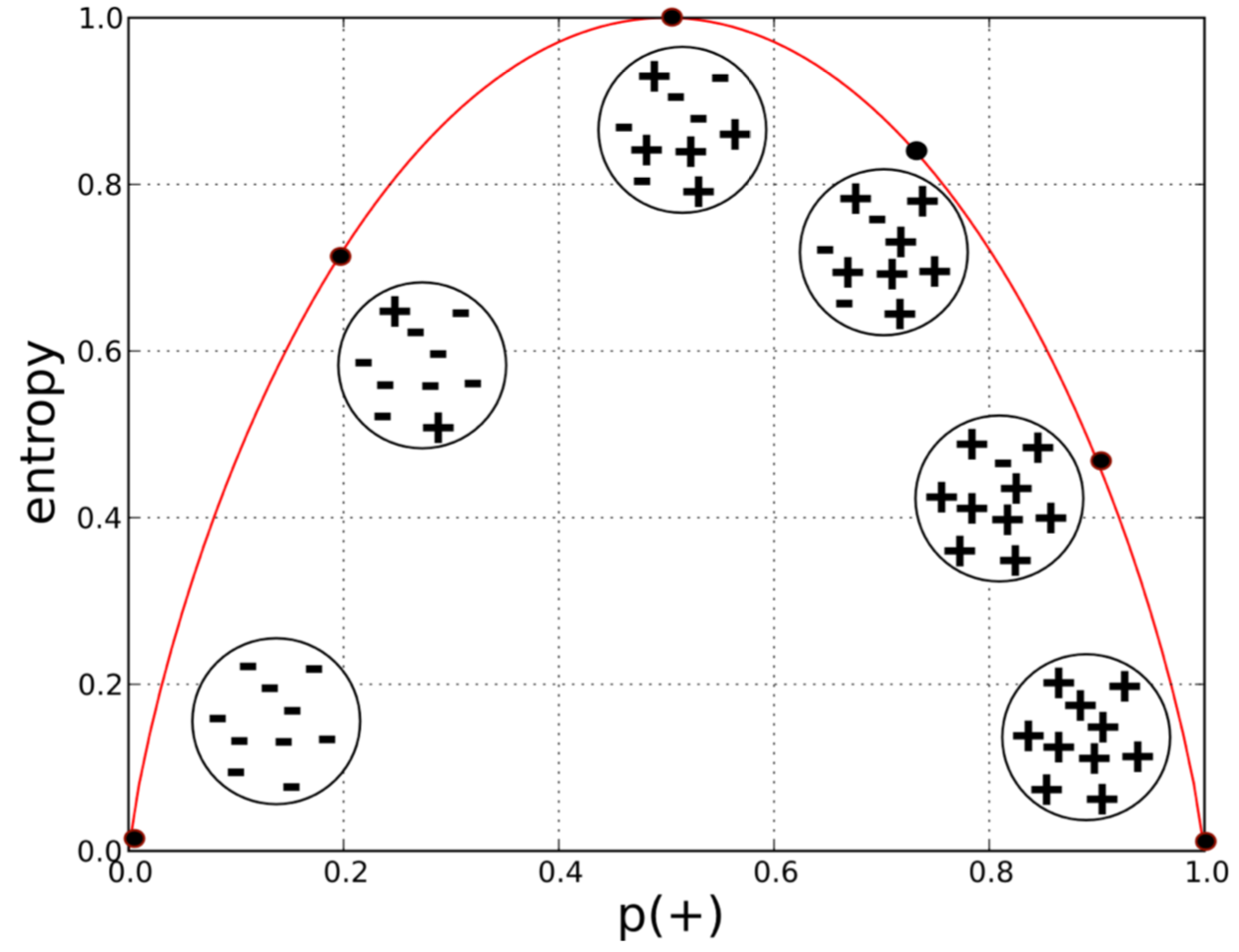
- 물리학에서 +전자와 -전자가 동률일때 가장 안정적이다. 고로 p(+)가 0.5일때 가장 안정적인 상태라고 볼 수 있음
(-전자가 1개가 많거나 +전자가 1개가 적으면 불안정하여 물질이 변환 될 수 있기떄문에)
- 하지만 데이터 분석쪽에서는 어떤 집단을 이진분류를 해놓고 뽑았더니 다 -전자거나, +전자이면 분류가 아주 잘된걸로 보이기 때문에 엔트로피가 0에 가까울수록 안정된 상태라고 볼 수 있다.
(아래의 표를 보면 p(+)가 0이거나 1일때 엔트로피가 0인것을 볼수가 있다. 데이터 분석쪽에선 이게 잘 분류된 것)
o 그럼 Entropy를 어떻게 계산을 할 것인가?
- 예시 ) 전체 고객 10명 중 정상 상환 고객이 7명이고, 미상환 고객이 3명이다.
p(정상상환) = 0.7 , p(미상환) = 0.3 으로 표현할 수 있고 이것은 엔트로피 구하는 공식에 대입하면된다.
엔트로피 구하는 공식 $$ (-p*log_2(p))+(-p*log_2(p)) $$
$$ (-0.7*log_2(0.7))+(-0.3*log_2(0.3)) $$ 아까 정상상환과 미상환을 대입하면 이런 식이 나온다.
추가로 $$ log_2(0.7) = log_{10}(0.7)/log_{10}(2) $$로 계산 가능하다.
정리하면 $$ = 0.7*0.51 + 0.3*1.7 $$ $$ = 0.36 + 0.52 $$ $$ = 0.88 $$로 정리할 수 있다.
값이 0.88이니까 1에 가까우니 이건 불안정한 것이다.
어떤 Attribute가 Target Value에 끼치는 영향력을 측정해봐야하는데,
엔트로피 계산할때 상환여부만 확인했다.
어떤 Attribute가 Target Value에 끼치는 영향력을 측정하기 위해 Information Gain(IG)를 추가한다. 왜 이걸 먼저 안한지는 엔트로피를 알아야할 수 있기 때문이다.
IG의 공식은 다음과 같다. $$ IG(parents, children) = $$ $$ entropy(parents) - [p(C_1) * entropy(C_1) + p(C_2) * entropy(C_2) + .....] $$
Entropy(parents)는 Target 값의 entorpy
수식의 의미를 파악하면 쉽다!
p(C1,C2)를 빼고보면 자녀의 엔트로피를 다 더해서 부모의 엔트로피에서 빼면된다.
부모엔트로피는 방금 위에서 계산한 0.88이 값이다. Target 값의 엔트로피여서 데이터만 구해지면 도출할 수 있다.
데이터 개수가 변하지 않는 이상 부모 엔트로피는 변하지 안흔ㄴ다.
자녀엔트로피는 무엇이고, 자녀는 무엇인가?
Information Gain(IG)이 진짜 영향력을 표현하는 식이다.
아까봤전 p(C1,C2)는 위표에 직장, 통장잔고 등이 해당 된다. 그러면 어떻게 계산하면 될것인가?
아래의 그림을 보고 예시로 계산을 해보자.

Entropy(부모)
$$ -0.53*log_2(0.53) + -0.47*log_2(0.47) $$ $$ = -[0.53*-0.9 + 0.47 * -1.1] $$ $$ = 0.99 $$
위의 식으로 부모의 엔트로피를 계산할 수 있다. 다음으로 통장잔고 1억이상 사람의 엔트로피를 구해보자
$$ -[0.92*log_2(0.92) + 0.08*log_2(0.08)] $$ $$ = -[0.92*-0.12 + 0.08 * -.3.7] $$ $$ =0.39 $$
이와같이 다음으로 통장잔고 1억 미만인 사람들의 엔트로피를 구해보자
$$ -[0.24*log_2(0.24) + 0.76*log_2(0.76)] $$ $$ = -[0.24 * -2.1 + 0.76 * -0.39] $$ $$ = 0.79 $$
정리하면
entropy(부모) - [p(통장잔고>=1억) * entropy(통장잔고>=1억) + p(통장잔고<1억) * entropy(통장잔고<1억)]
= 0.99 - [0.43*0.39+0.57*0.79]
= 0.37이 나온다.
(처음 보여줬던 p(c1,c2)의 값은 빠져있는건 아래에 설명)
ㅁ고민이 필요한 부분
o Entropy는 0에 가까울수록 안정적이고, Information Gain은 1에 가까울수록 안정적일 확률이 높고 Target Value에 끼치는 영향력이 큰 Attribute임
o 초급분석가들이 실수 하는 이유 중 하나는 홍길동 x 3하면 계산이 불가능하다. 이와 같이 Information Gain은 뭘 알아야 계산할 수 있을 것인가? -> 엔트로피를 알아야 계산할 수 있다 -> 엔트로피는 무엇을 알아야 계산할 수 있을까? -> 확률을 알아야 계싼할 수 있다. -> 확률은 어떻게 알 수있을까? -> 셀 수 있어야 계산할 수 있다.
o 확률 기반의 알고리즘을 활용할거라면 쓸 수 있는 데이터(셀 수 있는)이어야 쓸 수 있다.
o 내가 쓰는 알고리즘의 본질을 알아야하고, 전처리에 대한 필요성이 강조되는 부분이다.
o 통장잔고를 1억 기준으로 나눈 이유는 무엇일까?
- 이산형 데이터 : 숫자값인데 숫자값을 2개로 나눌 수 있다.
이산형 데이터는 주사위 돌리면 1-6으로 데이터의 크기가 정해져 있고 셀수가 있다.
- 연속형 데이터 : 시간, 나이, 돈 등을 연속형 데이터라고 하고 셀 수가 없고 끝이 없다.
숫자처럼 보이지만 셀 수 있는 데이터인지 셀 수 없는 데이터인지를 판단해야하고,
셀 수가 없으면 전처리를 거쳐야 한다. 많이 사용하는 전처리 방법은 구간화 시키는 것이다(1억 이상 등)
o 아까전에 계산했던 1억 기준이 바뀌면 확률도 바뀌고 값도 다 바뀌므로 전처리가 매우 중요하고, 이것을 자동화 할 수 있는 프로그래밍은 매우 중요하다.
o 극단적으로 통장잔고 1억 이상이 10개, 1억 미만이 9990개있다고 치고 엔트로피를 계산하면 1억 이상은 0에 가깝다. 1억 미만인 9990개에서 비율이 5:5라면 엔트로피 값이 거의 1에 가까워진다.
o 그렇기 때문에 아까 수식에서 p(c1,c2)를 빼고 계산하면 결과가 왜곡된다. 그래서 마지막으로 가중치를 곱해줘서 결과가 덜 왜곡되도록 보정하는 것이고, 그 가중치는 기울기로 인지하고 있으면 된다.
'Develop > AI' 카테고리의 다른 글
| 인공지능(신경망, 딥러닝) 교육 정리(Logistic Regression) (0) | 2023.01.01 |
|---|---|
| 인공지능(신경망, 딥러닝) 교육 정리 (Linear Regression) (0) | 2022.12.28 |
| 인공지능(신경망, 딥러닝) 교육 정리 [Linear Classifier] (0) | 2022.12.28 |
| 인공지능(신경망, 딥러닝) 교육 정리 [Decision Tree] (0) | 2022.12.28 |
| 인공지능(신경망, 딥러닝) 교육 정리 [개요] (0) | 2022.12.27 |








최근댓글